Getting started with MOM6
MOM6 variables are staggered according to the Arakawa C-grid
It uses a north-east index convention
center points are labelled (xh, yh) and corner points are labelled (xq, yq)
important: variables xh/yh, xq/yq that are named “nominal” longitude/latitude are not the true geographical coordinates and are not suitable for plotting (more later)
See indexing for details.
[1]:
import xarray as xr
from xgcm import Grid
import warnings
import matplotlib.pylab as plt
import cartopy.crs as ccrs
import cmocean
[2]:
%matplotlib inline
warnings.filterwarnings("ignore")
For this tutorial, we are going to use sample data for the \(\frac{1}{2}^{\circ}\) global model OM4p05 hosted on a GFDL thredds server:
[3]:
dataurl = 'http://35.188.34.63:8080/thredds/dodsC/OM4p5/'
ds = xr.open_dataset(f'{dataurl}/ocean_monthly_z.200301-200712.nc4',
chunks={'time':1, 'z_l': 1}, drop_variables=['average_DT',
'average_T1',
'average_T2'],
engine='pydap')
[4]:
ds
[4]:
<xarray.Dataset>
Dimensions: (nv: 2, time: 60, xh: 720, xq: 720, yh: 576, yq: 576, z_i: 36, z_l: 35)
Coordinates:
* nv (nv) float64 1.0 2.0
* xh (xh) float64 -299.8 -299.2 -298.8 -298.2 ... 58.75 59.25 59.75
* xq (xq) float64 -299.5 -299.0 -298.5 -298.0 ... 59.0 59.5 60.0
* yh (yh) float64 -77.91 -77.72 -77.54 -77.36 ... 89.47 89.68 89.89
* yq (yq) float64 -77.82 -77.63 -77.45 -77.26 ... 89.58 89.79 90.0
* z_i (z_i) float64 0.0 5.0 15.0 25.0 ... 5.75e+03 6.25e+03 6.75e+03
* z_l (z_l) float64 2.5 10.0 20.0 32.5 ... 5.5e+03 6e+03 6.5e+03
* time (time) object 2003-01-16 12:00:00 ... 2007-12-16 12:00:00
Data variables:
Coriolis (yq, xq) float32 dask.array<chunksize=(576, 720), meta=np.ndarray>
areacello (yh, xh) float32 dask.array<chunksize=(576, 720), meta=np.ndarray>
areacello_bu (yq, xq) float32 dask.array<chunksize=(576, 720), meta=np.ndarray>
areacello_cu (yh, xq) float32 dask.array<chunksize=(576, 720), meta=np.ndarray>
areacello_cv (yq, xh) float32 dask.array<chunksize=(576, 720), meta=np.ndarray>
deptho (yh, xh) float32 dask.array<chunksize=(576, 720), meta=np.ndarray>
dxCu (yh, xq) float32 dask.array<chunksize=(576, 720), meta=np.ndarray>
dxCv (yq, xh) float32 dask.array<chunksize=(576, 720), meta=np.ndarray>
dxt (yh, xh) float32 dask.array<chunksize=(576, 720), meta=np.ndarray>
dyCu (yh, xq) float32 dask.array<chunksize=(576, 720), meta=np.ndarray>
dyCv (yq, xh) float32 dask.array<chunksize=(576, 720), meta=np.ndarray>
dyt (yh, xh) float32 dask.array<chunksize=(576, 720), meta=np.ndarray>
geolat (yh, xh) float32 dask.array<chunksize=(576, 720), meta=np.ndarray>
geolat_c (yq, xq) float32 dask.array<chunksize=(576, 720), meta=np.ndarray>
geolat_u (yh, xq) float32 dask.array<chunksize=(576, 720), meta=np.ndarray>
geolat_v (yq, xh) float32 dask.array<chunksize=(576, 720), meta=np.ndarray>
geolon (yh, xh) float32 dask.array<chunksize=(576, 720), meta=np.ndarray>
geolon_c (yq, xq) float32 dask.array<chunksize=(576, 720), meta=np.ndarray>
geolon_u (yh, xq) float32 dask.array<chunksize=(576, 720), meta=np.ndarray>
geolon_v (yq, xh) float32 dask.array<chunksize=(576, 720), meta=np.ndarray>
hfgeou (yh, xh) float32 dask.array<chunksize=(576, 720), meta=np.ndarray>
sftof (yh, xh) float32 dask.array<chunksize=(576, 720), meta=np.ndarray>
thkcello (z_l, yh, xh) float32 dask.array<chunksize=(1, 576, 720), meta=np.ndarray>
wet (yh, xh) float32 dask.array<chunksize=(576, 720), meta=np.ndarray>
wet_c (yq, xq) float32 dask.array<chunksize=(576, 720), meta=np.ndarray>
wet_u (yh, xq) float32 dask.array<chunksize=(576, 720), meta=np.ndarray>
wet_v (yq, xh) float32 dask.array<chunksize=(576, 720), meta=np.ndarray>
so (time, z_l, yh, xh) float32 dask.array<chunksize=(1, 1, 576, 720), meta=np.ndarray>
time_bnds (time, nv) timedelta64[ns] dask.array<chunksize=(1, 2), meta=np.ndarray>
thetao (time, z_l, yh, xh) float32 dask.array<chunksize=(1, 1, 576, 720), meta=np.ndarray>
umo (time, z_l, yh, xq) float32 dask.array<chunksize=(1, 1, 576, 720), meta=np.ndarray>
uo (time, z_l, yh, xq) float32 dask.array<chunksize=(1, 1, 576, 720), meta=np.ndarray>
vmo (time, z_l, yq, xh) float32 dask.array<chunksize=(1, 1, 576, 720), meta=np.ndarray>
vo (time, z_l, yq, xh) float32 dask.array<chunksize=(1, 1, 576, 720), meta=np.ndarray>
volcello (time, z_l, yh, xh) float32 dask.array<chunksize=(1, 1, 576, 720), meta=np.ndarray>
zos (time, yh, xh) float32 dask.array<chunksize=(1, 576, 720), meta=np.ndarray>
Attributes:
filename: ocean_monthly.200301-200712.zos.nc
title: OM4p5_IAF_BLING_CFC_abio_csf_mle200
associated_files: areacello: 20030101.ocean_static.nc
grid_type: regular
grid_tile: N/A
external_variables: areacello
DODS_EXTRA.Unlimited_Dimension: time- nv: 2
- time: 60
- xh: 720
- xq: 720
- yh: 576
- yq: 576
- z_i: 36
- z_l: 35
- nv(nv)float641.0 2.0
- long_name :
- vertex number
- units :
- none
- cartesian_axis :
- N
- _ChunkSizes :
- 2
array([1., 2.])
- xh(xh)float64-299.8 -299.2 ... 59.25 59.75
- long_name :
- h point nominal longitude
- units :
- degrees_east
- cartesian_axis :
- X
- _ChunkSizes :
- 720
array([-299.75, -299.25, -298.75, ..., 58.75, 59.25, 59.75])
- xq(xq)float64-299.5 -299.0 -298.5 ... 59.5 60.0
- long_name :
- q point nominal longitude
- units :
- degrees_east
- cartesian_axis :
- X
- _ChunkSizes :
- 720
array([-299.5, -299. , -298.5, ..., 59. , 59.5, 60. ])
- yh(yh)float64-77.91 -77.72 ... 89.68 89.89
- long_name :
- h point nominal latitude
- units :
- degrees_north
- cartesian_axis :
- Y
- _ChunkSizes :
- 576
array([-77.907938, -77.723813, -77.539688, ..., 89.472 , 89.6832 , 89.8944 ]) - yq(yq)float64-77.82 -77.63 -77.45 ... 89.79 90.0
- long_name :
- q point nominal latitude
- units :
- degrees_north
- cartesian_axis :
- Y
- _ChunkSizes :
- 576
array([-77.815875, -77.63175 , -77.447625, ..., 89.5776 , 89.7888 , 90. ]) - z_i(z_i)float640.0 5.0 15.0 ... 6.25e+03 6.75e+03
- long_name :
- Depth at interface
- units :
- meters
- cartesian_axis :
- Z
- positive :
- down
- _ChunkSizes :
- 36
array([0.000e+00, 5.000e+00, 1.500e+01, 2.500e+01, 4.000e+01, 6.250e+01, 8.750e+01, 1.125e+02, 1.375e+02, 1.750e+02, 2.250e+02, 2.750e+02, 3.500e+02, 4.500e+02, 5.500e+02, 6.500e+02, 7.500e+02, 8.500e+02, 9.500e+02, 1.050e+03, 1.150e+03, 1.250e+03, 1.350e+03, 1.450e+03, 1.625e+03, 1.875e+03, 2.250e+03, 2.750e+03, 3.250e+03, 3.750e+03, 4.250e+03, 4.750e+03, 5.250e+03, 5.750e+03, 6.250e+03, 6.750e+03]) - z_l(z_l)float642.5 10.0 20.0 ... 6e+03 6.5e+03
- long_name :
- Depth at cell center
- units :
- meters
- cartesian_axis :
- Z
- positive :
- down
- edges :
- z_i
- _ChunkSizes :
- 35
array([2.5000e+00, 1.0000e+01, 2.0000e+01, 3.2500e+01, 5.1250e+01, 7.5000e+01, 1.0000e+02, 1.2500e+02, 1.5625e+02, 2.0000e+02, 2.5000e+02, 3.1250e+02, 4.0000e+02, 5.0000e+02, 6.0000e+02, 7.0000e+02, 8.0000e+02, 9.0000e+02, 1.0000e+03, 1.1000e+03, 1.2000e+03, 1.3000e+03, 1.4000e+03, 1.5375e+03, 1.7500e+03, 2.0625e+03, 2.5000e+03, 3.0000e+03, 3.5000e+03, 4.0000e+03, 4.5000e+03, 5.0000e+03, 5.5000e+03, 6.0000e+03, 6.5000e+03]) - time(time)object2003-01-16 12:00:00 ... 2007-12-...
- long_name :
- time
- cartesian_axis :
- T
- calendar_type :
- NOLEAP
- bounds :
- time_bnds
- _ChunkSizes :
- 512
array([cftime.DatetimeNoLeap(2003, 1, 16, 12, 0, 0, 0, 2, 16), cftime.DatetimeNoLeap(2003, 2, 15, 0, 0, 0, 0, 4, 46), cftime.DatetimeNoLeap(2003, 3, 16, 12, 0, 0, 0, 5, 75), cftime.DatetimeNoLeap(2003, 4, 16, 0, 0, 0, 0, 1, 106), cftime.DatetimeNoLeap(2003, 5, 16, 12, 0, 0, 0, 3, 136), cftime.DatetimeNoLeap(2003, 6, 16, 0, 0, 0, 0, 6, 167), cftime.DatetimeNoLeap(2003, 7, 16, 12, 0, 0, 0, 1, 197), cftime.DatetimeNoLeap(2003, 8, 16, 12, 0, 0, 0, 4, 228), cftime.DatetimeNoLeap(2003, 9, 16, 0, 0, 0, 0, 0, 259), cftime.DatetimeNoLeap(2003, 10, 16, 12, 0, 0, 0, 2, 289), cftime.DatetimeNoLeap(2003, 11, 16, 0, 0, 0, 0, 5, 320), cftime.DatetimeNoLeap(2003, 12, 16, 12, 0, 0, 0, 0, 350), cftime.DatetimeNoLeap(2004, 1, 16, 12, 0, 0, 0, 3, 16), cftime.DatetimeNoLeap(2004, 2, 15, 0, 0, 0, 0, 5, 46), cftime.DatetimeNoLeap(2004, 3, 16, 12, 0, 0, 0, 6, 75), cftime.DatetimeNoLeap(2004, 4, 16, 0, 0, 0, 0, 2, 106), cftime.DatetimeNoLeap(2004, 5, 16, 12, 0, 0, 0, 4, 136), cftime.DatetimeNoLeap(2004, 6, 16, 0, 0, 0, 0, 0, 167), cftime.DatetimeNoLeap(2004, 7, 16, 12, 0, 0, 0, 2, 197), cftime.DatetimeNoLeap(2004, 8, 16, 12, 0, 0, 0, 5, 228), cftime.DatetimeNoLeap(2004, 9, 16, 0, 0, 0, 0, 1, 259), cftime.DatetimeNoLeap(2004, 10, 16, 12, 0, 0, 0, 3, 289), cftime.DatetimeNoLeap(2004, 11, 16, 0, 0, 0, 0, 6, 320), cftime.DatetimeNoLeap(2004, 12, 16, 12, 0, 0, 0, 1, 350), cftime.DatetimeNoLeap(2005, 1, 16, 12, 0, 0, 0, 4, 16), cftime.DatetimeNoLeap(2005, 2, 15, 0, 0, 0, 0, 6, 46), cftime.DatetimeNoLeap(2005, 3, 16, 12, 0, 0, 0, 0, 75), cftime.DatetimeNoLeap(2005, 4, 16, 0, 0, 0, 0, 3, 106), cftime.DatetimeNoLeap(2005, 5, 16, 12, 0, 0, 0, 5, 136), cftime.DatetimeNoLeap(2005, 6, 16, 0, 0, 0, 0, 1, 167), cftime.DatetimeNoLeap(2005, 7, 16, 12, 0, 0, 0, 3, 197), cftime.DatetimeNoLeap(2005, 8, 16, 12, 0, 0, 0, 6, 228), cftime.DatetimeNoLeap(2005, 9, 16, 0, 0, 0, 0, 2, 259), cftime.DatetimeNoLeap(2005, 10, 16, 12, 0, 0, 0, 4, 289), cftime.DatetimeNoLeap(2005, 11, 16, 0, 0, 0, 0, 0, 320), cftime.DatetimeNoLeap(2005, 12, 16, 12, 0, 0, 0, 2, 350), cftime.DatetimeNoLeap(2006, 1, 16, 12, 0, 0, 0, 5, 16), cftime.DatetimeNoLeap(2006, 2, 15, 0, 0, 0, 0, 0, 46), cftime.DatetimeNoLeap(2006, 3, 16, 12, 0, 0, 0, 1, 75), cftime.DatetimeNoLeap(2006, 4, 16, 0, 0, 0, 0, 4, 106), cftime.DatetimeNoLeap(2006, 5, 16, 12, 0, 0, 0, 6, 136), cftime.DatetimeNoLeap(2006, 6, 16, 0, 0, 0, 0, 2, 167), cftime.DatetimeNoLeap(2006, 7, 16, 12, 0, 0, 0, 4, 197), cftime.DatetimeNoLeap(2006, 8, 16, 12, 0, 0, 0, 0, 228), cftime.DatetimeNoLeap(2006, 9, 16, 0, 0, 0, 0, 3, 259), cftime.DatetimeNoLeap(2006, 10, 16, 12, 0, 0, 0, 5, 289), cftime.DatetimeNoLeap(2006, 11, 16, 0, 0, 0, 0, 1, 320), cftime.DatetimeNoLeap(2006, 12, 16, 12, 0, 0, 0, 3, 350), cftime.DatetimeNoLeap(2007, 1, 16, 12, 0, 0, 0, 6, 16), cftime.DatetimeNoLeap(2007, 2, 15, 0, 0, 0, 0, 1, 46), cftime.DatetimeNoLeap(2007, 3, 16, 12, 0, 0, 0, 2, 75), cftime.DatetimeNoLeap(2007, 4, 16, 0, 0, 0, 0, 5, 106), cftime.DatetimeNoLeap(2007, 5, 16, 12, 0, 0, 0, 0, 136), cftime.DatetimeNoLeap(2007, 6, 16, 0, 0, 0, 0, 3, 167), cftime.DatetimeNoLeap(2007, 7, 16, 12, 0, 0, 0, 5, 197), cftime.DatetimeNoLeap(2007, 8, 16, 12, 0, 0, 0, 1, 228), cftime.DatetimeNoLeap(2007, 9, 16, 0, 0, 0, 0, 4, 259), cftime.DatetimeNoLeap(2007, 10, 16, 12, 0, 0, 0, 6, 289), cftime.DatetimeNoLeap(2007, 11, 16, 0, 0, 0, 0, 2, 320), cftime.DatetimeNoLeap(2007, 12, 16, 12, 0, 0, 0, 4, 350)], dtype=object)
- Coriolis(yq, xq)float32dask.array<chunksize=(576, 720), meta=np.ndarray>
- long_name :
- Coriolis parameter at corner (Bu) points
- units :
- s-1
- cell_methods :
- time: point
- interp_method :
- none
- _ChunkSizes :
- [576, 720]
Array Chunk Bytes 1.66 MB 1.66 MB Shape (576, 720) (576, 720) Count 2 Tasks 1 Chunks Type float32 numpy.ndarray - areacello(yh, xh)float32dask.array<chunksize=(576, 720), meta=np.ndarray>
- long_name :
- Ocean Grid-Cell Area
- units :
- m2
- cell_methods :
- area:sum yh:sum xh:sum time: point
- standard_name :
- cell_area
- _ChunkSizes :
- [576, 720]
Array Chunk Bytes 1.66 MB 1.66 MB Shape (576, 720) (576, 720) Count 2 Tasks 1 Chunks Type float32 numpy.ndarray - areacello_bu(yq, xq)float32dask.array<chunksize=(576, 720), meta=np.ndarray>
- long_name :
- Ocean Grid-Cell Area
- units :
- m2
- cell_methods :
- area:sum yq:sum xq:sum time: point
- standard_name :
- cell_area
- _ChunkSizes :
- [576, 720]
Array Chunk Bytes 1.66 MB 1.66 MB Shape (576, 720) (576, 720) Count 2 Tasks 1 Chunks Type float32 numpy.ndarray - areacello_cu(yh, xq)float32dask.array<chunksize=(576, 720), meta=np.ndarray>
- long_name :
- Ocean Grid-Cell Area
- units :
- m2
- cell_methods :
- area:sum yh:sum xq:sum time: point
- standard_name :
- cell_area
- _ChunkSizes :
- [576, 720]
Array Chunk Bytes 1.66 MB 1.66 MB Shape (576, 720) (576, 720) Count 2 Tasks 1 Chunks Type float32 numpy.ndarray - areacello_cv(yq, xh)float32dask.array<chunksize=(576, 720), meta=np.ndarray>
- long_name :
- Ocean Grid-Cell Area
- units :
- m2
- cell_methods :
- area:sum yq:sum xh:sum time: point
- standard_name :
- cell_area
- _ChunkSizes :
- [576, 720]
Array Chunk Bytes 1.66 MB 1.66 MB Shape (576, 720) (576, 720) Count 2 Tasks 1 Chunks Type float32 numpy.ndarray - deptho(yh, xh)float32dask.array<chunksize=(576, 720), meta=np.ndarray>
- long_name :
- Sea Floor Depth
- units :
- m
- cell_methods :
- area:mean yh:mean xh:mean time: point
- cell_measures :
- area: areacello
- standard_name :
- sea_floor_depth_below_geoid
- _ChunkSizes :
- [576, 720]
Array Chunk Bytes 1.66 MB 1.66 MB Shape (576, 720) (576, 720) Count 2 Tasks 1 Chunks Type float32 numpy.ndarray - dxCu(yh, xq)float32dask.array<chunksize=(576, 720), meta=np.ndarray>
- long_name :
- Delta(x) at u points (meter)
- units :
- m
- cell_methods :
- time: point
- interp_method :
- none
- _ChunkSizes :
- [576, 720]
Array Chunk Bytes 1.66 MB 1.66 MB Shape (576, 720) (576, 720) Count 2 Tasks 1 Chunks Type float32 numpy.ndarray - dxCv(yq, xh)float32dask.array<chunksize=(576, 720), meta=np.ndarray>
- long_name :
- Delta(x) at v points (meter)
- units :
- m
- cell_methods :
- time: point
- interp_method :
- none
- _ChunkSizes :
- [576, 720]
Array Chunk Bytes 1.66 MB 1.66 MB Shape (576, 720) (576, 720) Count 2 Tasks 1 Chunks Type float32 numpy.ndarray - dxt(yh, xh)float32dask.array<chunksize=(576, 720), meta=np.ndarray>
- long_name :
- Delta(x) at thickness/tracer points (meter)
- units :
- m
- cell_methods :
- time: point
- interp_method :
- none
- _ChunkSizes :
- [576, 720]
Array Chunk Bytes 1.66 MB 1.66 MB Shape (576, 720) (576, 720) Count 2 Tasks 1 Chunks Type float32 numpy.ndarray - dyCu(yh, xq)float32dask.array<chunksize=(576, 720), meta=np.ndarray>
- long_name :
- Delta(y) at u points (meter)
- units :
- m
- cell_methods :
- time: point
- interp_method :
- none
- _ChunkSizes :
- [576, 720]
Array Chunk Bytes 1.66 MB 1.66 MB Shape (576, 720) (576, 720) Count 2 Tasks 1 Chunks Type float32 numpy.ndarray - dyCv(yq, xh)float32dask.array<chunksize=(576, 720), meta=np.ndarray>
- long_name :
- Delta(y) at v points (meter)
- units :
- m
- cell_methods :
- time: point
- interp_method :
- none
- _ChunkSizes :
- [576, 720]
Array Chunk Bytes 1.66 MB 1.66 MB Shape (576, 720) (576, 720) Count 2 Tasks 1 Chunks Type float32 numpy.ndarray - dyt(yh, xh)float32dask.array<chunksize=(576, 720), meta=np.ndarray>
- long_name :
- Delta(y) at thickness/tracer points (meter)
- units :
- m
- cell_methods :
- time: point
- interp_method :
- none
- _ChunkSizes :
- [576, 720]
Array Chunk Bytes 1.66 MB 1.66 MB Shape (576, 720) (576, 720) Count 2 Tasks 1 Chunks Type float32 numpy.ndarray - geolat(yh, xh)float32dask.array<chunksize=(576, 720), meta=np.ndarray>
- long_name :
- Latitude of tracer (T) points
- units :
- degrees_north
- cell_methods :
- time: point
- _ChunkSizes :
- [576, 720]
Array Chunk Bytes 1.66 MB 1.66 MB Shape (576, 720) (576, 720) Count 2 Tasks 1 Chunks Type float32 numpy.ndarray - geolat_c(yq, xq)float32dask.array<chunksize=(576, 720), meta=np.ndarray>
- long_name :
- Latitude of corner (Bu) points
- units :
- degrees_north
- cell_methods :
- time: point
- interp_method :
- none
- _ChunkSizes :
- [576, 720]
Array Chunk Bytes 1.66 MB 1.66 MB Shape (576, 720) (576, 720) Count 2 Tasks 1 Chunks Type float32 numpy.ndarray - geolat_u(yh, xq)float32dask.array<chunksize=(576, 720), meta=np.ndarray>
- long_name :
- Latitude of zonal velocity (Cu) points
- units :
- degrees_north
- cell_methods :
- time: point
- interp_method :
- none
- _ChunkSizes :
- [576, 720]
Array Chunk Bytes 1.66 MB 1.66 MB Shape (576, 720) (576, 720) Count 2 Tasks 1 Chunks Type float32 numpy.ndarray - geolat_v(yq, xh)float32dask.array<chunksize=(576, 720), meta=np.ndarray>
- long_name :
- Latitude of meridional velocity (Cv) points
- units :
- degrees_north
- cell_methods :
- time: point
- interp_method :
- none
- _ChunkSizes :
- [576, 720]
Array Chunk Bytes 1.66 MB 1.66 MB Shape (576, 720) (576, 720) Count 2 Tasks 1 Chunks Type float32 numpy.ndarray - geolon(yh, xh)float32dask.array<chunksize=(576, 720), meta=np.ndarray>
- long_name :
- Longitude of tracer (T) points
- units :
- degrees_east
- cell_methods :
- time: point
- _ChunkSizes :
- [576, 720]
Array Chunk Bytes 1.66 MB 1.66 MB Shape (576, 720) (576, 720) Count 2 Tasks 1 Chunks Type float32 numpy.ndarray - geolon_c(yq, xq)float32dask.array<chunksize=(576, 720), meta=np.ndarray>
- long_name :
- Longitude of corner (Bu) points
- units :
- degrees_east
- cell_methods :
- time: point
- interp_method :
- none
- _ChunkSizes :
- [576, 720]
Array Chunk Bytes 1.66 MB 1.66 MB Shape (576, 720) (576, 720) Count 2 Tasks 1 Chunks Type float32 numpy.ndarray - geolon_u(yh, xq)float32dask.array<chunksize=(576, 720), meta=np.ndarray>
- long_name :
- Longitude of zonal velocity (Cu) points
- units :
- degrees_east
- cell_methods :
- time: point
- interp_method :
- none
- _ChunkSizes :
- [576, 720]
Array Chunk Bytes 1.66 MB 1.66 MB Shape (576, 720) (576, 720) Count 2 Tasks 1 Chunks Type float32 numpy.ndarray - geolon_v(yq, xh)float32dask.array<chunksize=(576, 720), meta=np.ndarray>
- long_name :
- Longitude of meridional velocity (Cv) points
- units :
- degrees_east
- cell_methods :
- time: point
- interp_method :
- none
- _ChunkSizes :
- [576, 720]
Array Chunk Bytes 1.66 MB 1.66 MB Shape (576, 720) (576, 720) Count 2 Tasks 1 Chunks Type float32 numpy.ndarray - hfgeou(yh, xh)float32dask.array<chunksize=(576, 720), meta=np.ndarray>
- long_name :
- Upward geothermal heat flux at sea floor
- units :
- W m-2
- cell_methods :
- area:mean yh:mean xh:mean time: point
- standard_name :
- upward_geothermal_heat_flux_at_sea_floor
- _ChunkSizes :
- [576, 720]
Array Chunk Bytes 1.66 MB 1.66 MB Shape (576, 720) (576, 720) Count 2 Tasks 1 Chunks Type float32 numpy.ndarray - sftof(yh, xh)float32dask.array<chunksize=(576, 720), meta=np.ndarray>
- long_name :
- Sea Area Fraction
- units :
- %
- cell_methods :
- area:mean yh:mean xh:mean time: point
- standard_name :
- SeaAreaFraction
- _ChunkSizes :
- [576, 720]
Array Chunk Bytes 1.66 MB 1.66 MB Shape (576, 720) (576, 720) Count 2 Tasks 1 Chunks Type float32 numpy.ndarray - thkcello(z_l, yh, xh)float32dask.array<chunksize=(1, 576, 720), meta=np.ndarray>
- id :
- thkcello
- name :
- thkcello
- units :
- m
- long_name :
- ocean model cell thickness
- original_name :
- cell_thickness
- standard_name :
- cell_thickness
- comment :
- thkcello is the nominal cell thickness in z* coordinates. The model actual thkcello is time-dependent and can be calculated as thkcello * ( deptho + zos ) / deptho
- _ChunkSizes :
- [12, 192, 240]
Array Chunk Bytes 58.06 MB 1.66 MB Shape (35, 576, 720) (1, 576, 720) Count 36 Tasks 35 Chunks Type float32 numpy.ndarray - wet(yh, xh)float32dask.array<chunksize=(576, 720), meta=np.ndarray>
- long_name :
- 0 if land, 1 if ocean at tracer points
- units :
- none
- cell_methods :
- time: point
- cell_measures :
- area: areacello
- _ChunkSizes :
- [576, 720]
Array Chunk Bytes 1.66 MB 1.66 MB Shape (576, 720) (576, 720) Count 2 Tasks 1 Chunks Type float32 numpy.ndarray - wet_c(yq, xq)float32dask.array<chunksize=(576, 720), meta=np.ndarray>
- long_name :
- 0 if land, 1 if ocean at corner (Bu) points
- units :
- none
- cell_methods :
- time: point
- interp_method :
- none
- _ChunkSizes :
- [576, 720]
Array Chunk Bytes 1.66 MB 1.66 MB Shape (576, 720) (576, 720) Count 2 Tasks 1 Chunks Type float32 numpy.ndarray - wet_u(yh, xq)float32dask.array<chunksize=(576, 720), meta=np.ndarray>
- long_name :
- 0 if land, 1 if ocean at zonal velocity (Cu) points
- units :
- none
- cell_methods :
- time: point
- interp_method :
- none
- _ChunkSizes :
- [576, 720]
Array Chunk Bytes 1.66 MB 1.66 MB Shape (576, 720) (576, 720) Count 2 Tasks 1 Chunks Type float32 numpy.ndarray - wet_v(yq, xh)float32dask.array<chunksize=(576, 720), meta=np.ndarray>
- long_name :
- 0 if land, 1 if ocean at meridional velocity (Cv) points
- units :
- none
- cell_methods :
- time: point
- interp_method :
- none
- _ChunkSizes :
- [576, 720]
Array Chunk Bytes 1.66 MB 1.66 MB Shape (576, 720) (576, 720) Count 2 Tasks 1 Chunks Type float32 numpy.ndarray - so(time, z_l, yh, xh)float32dask.array<chunksize=(1, 1, 576, 720), meta=np.ndarray>
- long_name :
- Sea Water Salinity
- units :
- psu
- cell_methods :
- area:mean z_l:mean yh:mean xh:mean time: mean
- cell_measures :
- volume: volcello area: areacello
- time_avg_info :
- average_T1,average_T2,average_DT
- standard_name :
- sea_water_salinity
- _ChunkSizes :
- [1, 12, 192, 240]
Array Chunk Bytes 3.48 GB 1.66 MB Shape (60, 35, 576, 720) (1, 1, 576, 720) Count 2101 Tasks 2100 Chunks Type float32 numpy.ndarray - time_bnds(time, nv)timedelta64[ns]dask.array<chunksize=(1, 2), meta=np.ndarray>
- long_name :
- time axis boundaries
- _ChunkSizes :
- [1, 2]
- calendar :
- NOLEAP
Array Chunk Bytes 960 B 16 B Shape (60, 2) (1, 2) Count 61 Tasks 60 Chunks Type timedelta64[ns] numpy.ndarray - thetao(time, z_l, yh, xh)float32dask.array<chunksize=(1, 1, 576, 720), meta=np.ndarray>
- long_name :
- Sea Water Potential Temperature
- units :
- degC
- cell_methods :
- area:mean z_l:mean yh:mean xh:mean time: mean
- cell_measures :
- volume: volcello area: areacello
- time_avg_info :
- average_T1,average_T2,average_DT
- standard_name :
- sea_water_potential_temperature
- _ChunkSizes :
- [1, 12, 192, 240]
Array Chunk Bytes 3.48 GB 1.66 MB Shape (60, 35, 576, 720) (1, 1, 576, 720) Count 2101 Tasks 2100 Chunks Type float32 numpy.ndarray - umo(time, z_l, yh, xq)float32dask.array<chunksize=(1, 1, 576, 720), meta=np.ndarray>
- long_name :
- Ocean Mass X Transport
- units :
- kg s-1
- cell_methods :
- z_l:sum yh:sum xq:point time: mean
- time_avg_info :
- average_T1,average_T2,average_DT
- standard_name :
- ocean_mass_x_transport
- interp_method :
- none
- _ChunkSizes :
- [1, 12, 192, 240]
Array Chunk Bytes 3.48 GB 1.66 MB Shape (60, 35, 576, 720) (1, 1, 576, 720) Count 2101 Tasks 2100 Chunks Type float32 numpy.ndarray - uo(time, z_l, yh, xq)float32dask.array<chunksize=(1, 1, 576, 720), meta=np.ndarray>
- long_name :
- Sea Water X Velocity
- units :
- m s-1
- cell_methods :
- z_l:mean yh:mean xq:point time: mean
- time_avg_info :
- average_T1,average_T2,average_DT
- standard_name :
- sea_water_x_velocity
- interp_method :
- none
- _ChunkSizes :
- [1, 12, 192, 240]
Array Chunk Bytes 3.48 GB 1.66 MB Shape (60, 35, 576, 720) (1, 1, 576, 720) Count 2101 Tasks 2100 Chunks Type float32 numpy.ndarray - vmo(time, z_l, yq, xh)float32dask.array<chunksize=(1, 1, 576, 720), meta=np.ndarray>
- long_name :
- Ocean Mass Y Transport
- units :
- kg s-1
- cell_methods :
- z_l:sum yq:point xh:sum time: mean
- time_avg_info :
- average_T1,average_T2,average_DT
- standard_name :
- ocean_mass_y_transport
- interp_method :
- none
- _ChunkSizes :
- [1, 12, 192, 240]
Array Chunk Bytes 3.48 GB 1.66 MB Shape (60, 35, 576, 720) (1, 1, 576, 720) Count 2101 Tasks 2100 Chunks Type float32 numpy.ndarray - vo(time, z_l, yq, xh)float32dask.array<chunksize=(1, 1, 576, 720), meta=np.ndarray>
- long_name :
- Sea Water Y Velocity
- units :
- m s-1
- cell_methods :
- z_l:mean yq:point xh:mean time: mean
- time_avg_info :
- average_T1,average_T2,average_DT
- standard_name :
- sea_water_y_velocity
- interp_method :
- none
- _ChunkSizes :
- [1, 12, 192, 240]
Array Chunk Bytes 3.48 GB 1.66 MB Shape (60, 35, 576, 720) (1, 1, 576, 720) Count 2101 Tasks 2100 Chunks Type float32 numpy.ndarray - volcello(time, z_l, yh, xh)float32dask.array<chunksize=(1, 1, 576, 720), meta=np.ndarray>
- long_name :
- Ocean grid-cell volume
- units :
- m3
- cell_methods :
- area:sum z_l:sum yh:sum xh:sum time: mean
- cell_measures :
- area: areacello
- time_avg_info :
- average_T1,average_T2,average_DT
- standard_name :
- ocean_volume
- _ChunkSizes :
- [1, 12, 192, 240]
Array Chunk Bytes 3.48 GB 1.66 MB Shape (60, 35, 576, 720) (1, 1, 576, 720) Count 2101 Tasks 2100 Chunks Type float32 numpy.ndarray - zos(time, yh, xh)float32dask.array<chunksize=(1, 576, 720), meta=np.ndarray>
- long_name :
- Sea surface height above geoid
- units :
- m
- cell_methods :
- area:mean yh:mean xh:mean time: mean
- cell_measures :
- area: areacello
- time_avg_info :
- average_T1,average_T2,average_DT
- standard_name :
- sea_surface_height_above_geoid
- _ChunkSizes :
- [1, 576, 720]
Array Chunk Bytes 99.53 MB 1.66 MB Shape (60, 576, 720) (1, 576, 720) Count 61 Tasks 60 Chunks Type float32 numpy.ndarray
- filename :
- ocean_monthly.200301-200712.zos.nc
- title :
- OM4p5_IAF_BLING_CFC_abio_csf_mle200
- associated_files :
- areacello: 20030101.ocean_static.nc
- grid_type :
- regular
- grid_tile :
- N/A
- external_variables :
- areacello
- DODS_EXTRA.Unlimited_Dimension :
- time
Grid variables
The horizontal dimensions are a combination of (
xhorxq) and (yhoryq) corresponding to the staggered point. In the verticalz_lrefers to the depth of the center of the layer andz_ito the position of the interfaces, such aslen(z_i) = len(z_l) + 1.the
geolon/geolatfamily are the TRUE geographical coordinates and are the longitude/latitude you want to use to plot results. The subscript correspond to the staggered point (c: corner, u: U-point, v: V-point, no subscript: center)the
areacellofamily is the horizontal area of the ocean cell at various points with a slightly naming convention (bu: corner, cu: U-point, cv: V-point, no subscript: center). Since the grid cells are irregular, it is worth noting thatareacello≠dxt * dytthe
dx/dyfamily has the following naming convention:dx(Cu: U-point, Cv: V-point, no suffix: center)thkcellois the layer thickness for each cell (variable). volcello is the volume of the cell, such as:volcello = areacello * thkcello
The MOM6 output can be written in symmetric (len(Xq) = len(Xh) + 1) or non-symmetric mode (len(Xq) = len(Xh)), where X is a notation for both x and y.
Building an xgcm grid object
xgcm adds staggered grid information to xarray. To use its functionalities, one must define an xgcm grid object. In symmetric mode, one would define the grid for the global as:
grid = Grid(ds, coords={'X': {'inner': 'xh', 'outer': 'xq'},
'Y': {'inner': 'yh', 'outer': 'yq'},
'Z': {'inner': 'z_l', 'outer': 'z_i'} }, periodic=['X'])
and in non-symmetric mode:
grid = Grid(ds, coords={'X': {'center': 'xh', 'right': 'xq'},
'Y': {'center': 'yh', 'right': 'yq'},
'Z': {'inner': 'z_l', 'outer': 'z_i'} }, periodic=['X'])
Of course, do not forget to drop the periodic option if you are running a regional model. Our data is written in non-symmetric mode hence:
[5]:
grid = Grid(ds, coords={'X': {'center': 'xh', 'right': 'xq'},
'Y': {'center': 'yh', 'right': 'yq'},
'Z': {'inner': 'z_l', 'outer': 'z_i'} }, periodic=['X'])
A note on geographical coordinates
MOM6 uses land processor elimination, which creates blank holes in the produced geolon/geolat fields. This can result in problems while plotting. It is recommended to overwrite them by the full arrays that are produced by running the model for a few steps without land processor elimination. Here we copy one of these files.
[6]:
ocean_grid_sym = xr.open_dataset('./data/ocean_grid_sym_OM4_05.nc')
[7]:
ocean_grid_sym
[7]:
<xarray.Dataset>
Dimensions: (xh: 720, xq: 721, yh: 576, yq: 577)
Coordinates:
* xh (xh) float64 -299.8 -299.2 -298.8 -298.2 ... 58.75 59.25 59.75
* xq (xq) float64 -300.0 -299.5 -299.0 -298.5 ... 58.5 59.0 59.5 60.0
* yh (yh) float64 -77.91 -77.72 -77.54 -77.36 ... 89.47 89.68 89.89
* yq (yq) float64 -78.0 -77.82 -77.63 -77.45 ... 89.37 89.58 89.79 90.0
Data variables:
geolat (yh, xh) float32 ...
geolat_c (yq, xq) float32 ...
geolon (yh, xh) float32 ...
geolon_c (yq, xq) float32 ...
Attributes:
filename: 19000101.ocean_static.nc
title: OM4_SIS2_cgrid_05
grid_type: regular
grid_tile: N/A
history: Tue Mar 3 13:41:58 2020: ncks -v geolon,geolon_c,geolat,geol...
NCO: 4.0.3- xh: 720
- xq: 721
- yh: 576
- yq: 577
- xh(xh)float64-299.8 -299.2 ... 59.25 59.75
- long_name :
- h point nominal longitude
- units :
- degrees_east
- cartesian_axis :
- X
array([-299.75, -299.25, -298.75, ..., 58.75, 59.25, 59.75])
- xq(xq)float64-300.0 -299.5 -299.0 ... 59.5 60.0
- long_name :
- q point nominal longitude
- units :
- degrees_east
- cartesian_axis :
- X
array([-300. , -299.5, -299. , ..., 59. , 59.5, 60. ])
- yh(yh)float64-77.91 -77.72 ... 89.68 89.89
- long_name :
- h point nominal latitude
- units :
- degrees_north
- cartesian_axis :
- Y
array([-77.907938, -77.723813, -77.539688, ..., 89.472 , 89.6832 , 89.8944 ]) - yq(yq)float64-78.0 -77.82 -77.63 ... 89.79 90.0
- long_name :
- q point nominal latitude
- units :
- degrees_north
- cartesian_axis :
- Y
array([-78. , -77.815875, -77.63175 , ..., 89.5776 , 89.7888 , 90. ])
- geolat(yh, xh)float32...
- long_name :
- Latitude of tracer (T) points
- units :
- degrees_north
- cell_methods :
- time: point
[414720 values with dtype=float32]
- geolat_c(yq, xq)float32...
- long_name :
- Latitude of corner (Bu) points
- units :
- degrees_north
- cell_methods :
- time: point
- interp_method :
- none
[416017 values with dtype=float32]
- geolon(yh, xh)float32...
- long_name :
- Longitude of tracer (T) points
- units :
- degrees_east
- cell_methods :
- time: point
[414720 values with dtype=float32]
- geolon_c(yq, xq)float32...
- long_name :
- Longitude of corner (Bu) points
- units :
- degrees_east
- cell_methods :
- time: point
- interp_method :
- none
[416017 values with dtype=float32]
- filename :
- 19000101.ocean_static.nc
- title :
- OM4_SIS2_cgrid_05
- grid_type :
- regular
- grid_tile :
- N/A
- history :
- Tue Mar 3 13:41:58 2020: ncks -v geolon,geolon_c,geolat,geolat_c /archive/gold/datasets/OM4_05/mosaic_ocean.v20180227.unpacked/ocean_static_sym.nc -o ocean_grid_sym_OM5_05.nc
- NCO :
- 4.0.3
I took here a symetric grid for the purpose of showing the differences. Since this grid is symetric and MOM6 uses the north-east convention, we need to remove the first row and column in our arrays.
To overwrite our “gruyere” coordinates in our Non-symetric dataset, we can do:
[8]:
ds['geolon_c'] = xr.DataArray(data=ocean_grid_sym['geolon_c'][1:,1:], dims=('yq', 'xq'))
ds['geolat_c'] = xr.DataArray(data=ocean_grid_sym['geolat_c'][1:,1:], dims=('yq', 'xq'))
ds['geolon'] = xr.DataArray(data=ocean_grid_sym['geolon'], dims=('yh', 'xh'))
ds['geolat'] = xr.DataArray(data=ocean_grid_sym['geolat'], dims=('yh', 'xh'))
Plotting
To be able to plot using true longitude and latitude, we need to make geolon/geolat coordinates of the xarray.Dataset:
[9]:
ds = ds.assign_coords({'geolon': ds['geolon'],
'geolat': ds['geolat']})
Now notice the difference in the arctic between nominal (bad) coordinates and the true coordinates:
[10]:
ds['thetao'].isel(time=0, z_l=0).plot(vmin=-2, vmax=32,
cmap=cmocean.cm.thermal,
figsize=[10, 6])
[10]:
<matplotlib.collections.QuadMesh at 0x7f04a86f0588>
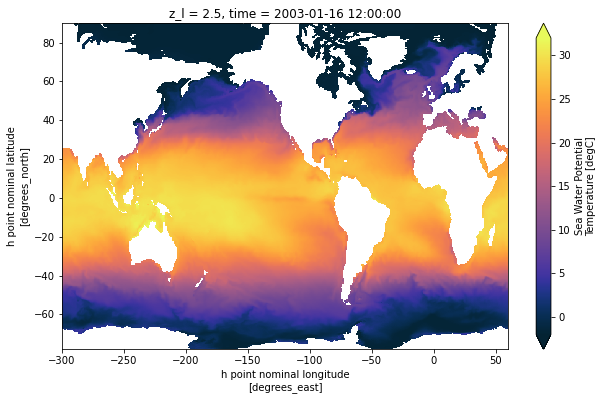
[11]:
ds['thetao'].isel(time=0, z_l=0).plot(vmin=-2, vmax=32,
x='geolon', y='geolat',
cmap=cmocean.cm.thermal,
figsize=[10, 6])
[11]:
<matplotlib.collections.QuadMesh at 0x7f04a85bb860>
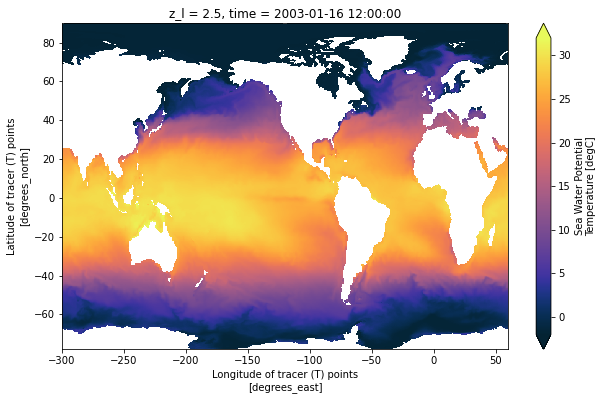
More control on xarray plot
Using the latest xarray >= 0.16.0, you can now adjust plot properties more easily:
[12]:
plt.figure(figsize=[14, 6])
p = ds['thetao'].isel(time=0, z_l=0).plot(vmin=-2, vmax=32,
x='geolon', y='geolat',
cmap=cmocean.cm.thermal,
subplot_kws={'projection': ccrs.Robinson(),
'facecolor':'grey'},
transform=ccrs.PlateCarree(),
add_labels=False,
add_colorbar=False)
p.axes.coastlines()
p.axes.gridlines(color='black', alpha=0.5, linestyle='--')
# add separate colorbar
cb = plt.colorbar(p, ticks=[0,5,10,15,20,25,30], shrink=0.95)
cb.ax.tick_params(labelsize=18)
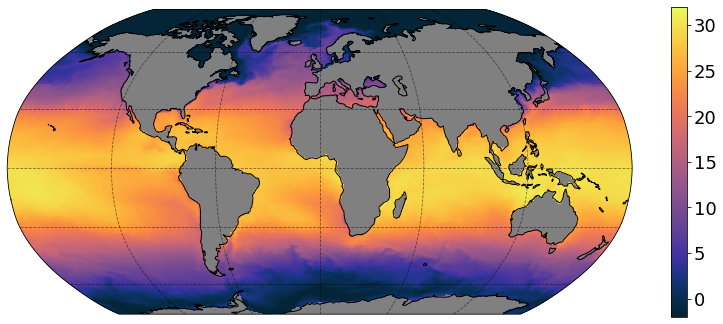
More plotting examples in the plotting section of the cookbook!