Spatial Operations

This notebook shows how to do some spatial operations. We focus here on averaging, since the sums can easily be infered.

[1]:

import xarray as xr # requires >= 0.15.1
import numpy as np

[2]:

import warnings
warnings.filterwarnings("ignore")

[3]:

%matplotlib inline

This is where you can find the dataset on the opendap (unfortunately parallel computing with dask won’t work)

dataurl = 'http://35.188.34.63:8080/thredds/dodsC/OM4p5/'

ds = xr.open_dataset(f'{dataurl}/ocean_monthly_z.200301-200712.nc4',
                     chunks={'time':1, 'z_l': 1}, engine='pydap')

I am using my local copy:

[4]:

dataurl = '/work/Raphael.Dussin/runs/OM4p5_sample/'

ds = xr.open_dataset(f'{dataurl}/ocean_monthly_z.200301-200712.nc4',
                     chunks={'time':1, 'z_l': 1}, engine='netcdf4')

[5]:

ds

[5]:

xarray.Dataset

Dimensions:
- nv: 2
- time: 60
- xh: 720
- xq: 720
- yh: 576
- yq: 576
- z_i: 36
- z_l: 35

Coordinates: (8)

Data variables: (39)

Coriolis

(yq, xq)

float32

dask.array<chunksize=(576, 720), meta=np.ndarray>

long_name :: Coriolis parameter at corner (Bu) points
units :: s-1
cell_methods :: time: point
interp_method :: none





  
      Array  Chunk 
  
  
     Bytes  1.66 MB   1.66 MB 
     Shape  (576, 720)   (576, 720) 
     Count  2 Tasks  1 Chunks 
     Type  float32  numpy.ndarray

areacello

(yh, xh)

float32

dask.array<chunksize=(576, 720), meta=np.ndarray>

long_name :: Ocean Grid-Cell Area
units :: m2
cell_methods :: area:sum yh:sum xh:sum time: point
standard_name :: cell_area





  
      Array  Chunk 
  
  
     Bytes  1.66 MB   1.66 MB 
     Shape  (576, 720)   (576, 720) 
     Count  2 Tasks  1 Chunks 
     Type  float32  numpy.ndarray

areacello_bu

(yq, xq)

float32

dask.array<chunksize=(576, 720), meta=np.ndarray>

long_name :: Ocean Grid-Cell Area
units :: m2
cell_methods :: area:sum yq:sum xq:sum time: point
standard_name :: cell_area





  
      Array  Chunk 
  
  
     Bytes  1.66 MB   1.66 MB 
     Shape  (576, 720)   (576, 720) 
     Count  2 Tasks  1 Chunks 
     Type  float32  numpy.ndarray

areacello_cu

(yh, xq)

float32

dask.array<chunksize=(576, 720), meta=np.ndarray>

long_name :: Ocean Grid-Cell Area
units :: m2
cell_methods :: area:sum yh:sum xq:sum time: point
standard_name :: cell_area





  
      Array  Chunk 
  
  
     Bytes  1.66 MB   1.66 MB 
     Shape  (576, 720)   (576, 720) 
     Count  2 Tasks  1 Chunks 
     Type  float32  numpy.ndarray

areacello_cv

(yq, xh)

float32

dask.array<chunksize=(576, 720), meta=np.ndarray>

long_name :: Ocean Grid-Cell Area
units :: m2
cell_methods :: area:sum yq:sum xh:sum time: point
standard_name :: cell_area





  
      Array  Chunk 
  
  
     Bytes  1.66 MB   1.66 MB 
     Shape  (576, 720)   (576, 720) 
     Count  2 Tasks  1 Chunks 
     Type  float32  numpy.ndarray

deptho

(yh, xh)

float32

dask.array<chunksize=(576, 720), meta=np.ndarray>

long_name :: Sea Floor Depth
units :: m
cell_methods :: area:mean yh:mean xh:mean time: point
cell_measures :: area: areacello
standard_name :: sea_floor_depth_below_geoid





  
      Array  Chunk 
  
  
     Bytes  1.66 MB   1.66 MB 
     Shape  (576, 720)   (576, 720) 
     Count  2 Tasks  1 Chunks 
     Type  float32  numpy.ndarray

dxCu

(yh, xq)

float32

dask.array<chunksize=(576, 720), meta=np.ndarray>

long_name :: Delta(x) at u points (meter)
units :: m
cell_methods :: time: point
interp_method :: none





  
      Array  Chunk 
  
  
     Bytes  1.66 MB   1.66 MB 
     Shape  (576, 720)   (576, 720) 
     Count  2 Tasks  1 Chunks 
     Type  float32  numpy.ndarray

dxCv

(yq, xh)

float32

dask.array<chunksize=(576, 720), meta=np.ndarray>

long_name :: Delta(x) at v points (meter)
units :: m
cell_methods :: time: point
interp_method :: none





  
      Array  Chunk 
  
  
     Bytes  1.66 MB   1.66 MB 
     Shape  (576, 720)   (576, 720) 
     Count  2 Tasks  1 Chunks 
     Type  float32  numpy.ndarray

dxt

(yh, xh)

float32

dask.array<chunksize=(576, 720), meta=np.ndarray>

long_name :: Delta(x) at thickness/tracer points (meter)
units :: m
cell_methods :: time: point
interp_method :: none





  
      Array  Chunk 
  
  
     Bytes  1.66 MB   1.66 MB 
     Shape  (576, 720)   (576, 720) 
     Count  2 Tasks  1 Chunks 
     Type  float32  numpy.ndarray

dyCu

(yh, xq)

float32

dask.array<chunksize=(576, 720), meta=np.ndarray>

long_name :: Delta(y) at u points (meter)
units :: m
cell_methods :: time: point
interp_method :: none





  
      Array  Chunk 
  
  
     Bytes  1.66 MB   1.66 MB 
     Shape  (576, 720)   (576, 720) 
     Count  2 Tasks  1 Chunks 
     Type  float32  numpy.ndarray

dyCv

(yq, xh)

float32

dask.array<chunksize=(576, 720), meta=np.ndarray>

long_name :: Delta(y) at v points (meter)
units :: m
cell_methods :: time: point
interp_method :: none





  
      Array  Chunk 
  
  
     Bytes  1.66 MB   1.66 MB 
     Shape  (576, 720)   (576, 720) 
     Count  2 Tasks  1 Chunks 
     Type  float32  numpy.ndarray

dyt

(yh, xh)

float32

dask.array<chunksize=(576, 720), meta=np.ndarray>

long_name :: Delta(y) at thickness/tracer points (meter)
units :: m
cell_methods :: time: point
interp_method :: none





  
      Array  Chunk 
  
  
     Bytes  1.66 MB   1.66 MB 
     Shape  (576, 720)   (576, 720) 
     Count  2 Tasks  1 Chunks 
     Type  float32  numpy.ndarray

geolat

(yh, xh)

float32

dask.array<chunksize=(576, 720), meta=np.ndarray>

long_name :: Latitude of tracer (T) points
units :: degrees_north
cell_methods :: time: point





  
      Array  Chunk 
  
  
     Bytes  1.66 MB   1.66 MB 
     Shape  (576, 720)   (576, 720) 
     Count  2 Tasks  1 Chunks 
     Type  float32  numpy.ndarray

geolat_c

(yq, xq)

float32

dask.array<chunksize=(576, 720), meta=np.ndarray>

long_name :: Latitude of corner (Bu) points
units :: degrees_north
cell_methods :: time: point
interp_method :: none





  
      Array  Chunk 
  
  
     Bytes  1.66 MB   1.66 MB 
     Shape  (576, 720)   (576, 720) 
     Count  2 Tasks  1 Chunks 
     Type  float32  numpy.ndarray

geolat_u

(yh, xq)

float32

dask.array<chunksize=(576, 720), meta=np.ndarray>

long_name :: Latitude of zonal velocity (Cu) points
units :: degrees_north
cell_methods :: time: point
interp_method :: none





  
      Array  Chunk 
  
  
     Bytes  1.66 MB   1.66 MB 
     Shape  (576, 720)   (576, 720) 
     Count  2 Tasks  1 Chunks 
     Type  float32  numpy.ndarray

geolat_v

(yq, xh)

float32

dask.array<chunksize=(576, 720), meta=np.ndarray>

long_name :: Latitude of meridional velocity (Cv) points
units :: degrees_north
cell_methods :: time: point
interp_method :: none





  
      Array  Chunk 
  
  
     Bytes  1.66 MB   1.66 MB 
     Shape  (576, 720)   (576, 720) 
     Count  2 Tasks  1 Chunks 
     Type  float32  numpy.ndarray

geolon

(yh, xh)

float32

dask.array<chunksize=(576, 720), meta=np.ndarray>

long_name :: Longitude of tracer (T) points
units :: degrees_east
cell_methods :: time: point





  
      Array  Chunk 
  
  
     Bytes  1.66 MB   1.66 MB 
     Shape  (576, 720)   (576, 720) 
     Count  2 Tasks  1 Chunks 
     Type  float32  numpy.ndarray

geolon_c

(yq, xq)

float32

dask.array<chunksize=(576, 720), meta=np.ndarray>

long_name :: Longitude of corner (Bu) points
units :: degrees_east
cell_methods :: time: point
interp_method :: none





  
      Array  Chunk 
  
  
     Bytes  1.66 MB   1.66 MB 
     Shape  (576, 720)   (576, 720) 
     Count  2 Tasks  1 Chunks 
     Type  float32  numpy.ndarray

geolon_u

(yh, xq)

float32

dask.array<chunksize=(576, 720), meta=np.ndarray>

long_name :: Longitude of zonal velocity (Cu) points
units :: degrees_east
cell_methods :: time: point
interp_method :: none





  
      Array  Chunk 
  
  
     Bytes  1.66 MB   1.66 MB 
     Shape  (576, 720)   (576, 720) 
     Count  2 Tasks  1 Chunks 
     Type  float32  numpy.ndarray

geolon_v

(yq, xh)

float32

dask.array<chunksize=(576, 720), meta=np.ndarray>

long_name :: Longitude of meridional velocity (Cv) points
units :: degrees_east
cell_methods :: time: point
interp_method :: none





  
      Array  Chunk 
  
  
     Bytes  1.66 MB   1.66 MB 
     Shape  (576, 720)   (576, 720) 
     Count  2 Tasks  1 Chunks 
     Type  float32  numpy.ndarray

hfgeou

(yh, xh)

float32

dask.array<chunksize=(576, 720), meta=np.ndarray>

long_name :: Upward geothermal heat flux at sea floor
units :: W m-2
cell_methods :: area:mean yh:mean xh:mean time: point
standard_name :: upward_geothermal_heat_flux_at_sea_floor





  
      Array  Chunk 
  
  
     Bytes  1.66 MB   1.66 MB 
     Shape  (576, 720)   (576, 720) 
     Count  2 Tasks  1 Chunks 
     Type  float32  numpy.ndarray

sftof

(yh, xh)

float32

dask.array<chunksize=(576, 720), meta=np.ndarray>

long_name :: Sea Area Fraction
units :: %
cell_methods :: area:mean yh:mean xh:mean time: point
standard_name :: SeaAreaFraction





  
      Array  Chunk 
  
  
     Bytes  1.66 MB   1.66 MB 
     Shape  (576, 720)   (576, 720) 
     Count  2 Tasks  1 Chunks 
     Type  float32  numpy.ndarray

thkcello

(z_l, yh, xh)

float32

dask.array<chunksize=(1, 576, 720), meta=np.ndarray>

id :: thkcello
name :: thkcello
units :: m
long_name :: ocean model cell thickness
original_name :: cell_thickness
standard_name :: cell_thickness
comment :: thkcello is the nominal cell thickness in z* coordinates. The model actual thkcello is time-dependent and can be calculated as thkcello * ( deptho + zos ) / deptho





  
      Array  Chunk 
  
  
     Bytes  58.06 MB   1.66 MB 
     Shape  (35, 576, 720)   (1, 576, 720) 
     Count  36 Tasks  35 Chunks 
     Type  float32  numpy.ndarray

wet

(yh, xh)

float32

dask.array<chunksize=(576, 720), meta=np.ndarray>

long_name :: 0 if land, 1 if ocean at tracer points
units :: none
cell_methods :: time: point
cell_measures :: area: areacello





  
      Array  Chunk 
  
  
     Bytes  1.66 MB   1.66 MB 
     Shape  (576, 720)   (576, 720) 
     Count  2 Tasks  1 Chunks 
     Type  float32  numpy.ndarray

wet_c

(yq, xq)

float32

dask.array<chunksize=(576, 720), meta=np.ndarray>

long_name :: 0 if land, 1 if ocean at corner (Bu) points
units :: none
cell_methods :: time: point
interp_method :: none





  
      Array  Chunk 
  
  
     Bytes  1.66 MB   1.66 MB 
     Shape  (576, 720)   (576, 720) 
     Count  2 Tasks  1 Chunks 
     Type  float32  numpy.ndarray

wet_u

(yh, xq)

float32

dask.array<chunksize=(576, 720), meta=np.ndarray>

long_name :: 0 if land, 1 if ocean at zonal velocity (Cu) points
units :: none
cell_methods :: time: point
interp_method :: none





  
      Array  Chunk 
  
  
     Bytes  1.66 MB   1.66 MB 
     Shape  (576, 720)   (576, 720) 
     Count  2 Tasks  1 Chunks 
     Type  float32  numpy.ndarray

wet_v

(yq, xh)

float32

dask.array<chunksize=(576, 720), meta=np.ndarray>

long_name :: 0 if land, 1 if ocean at meridional velocity (Cv) points
units :: none
cell_methods :: time: point
interp_method :: none





  
      Array  Chunk 
  
  
     Bytes  1.66 MB   1.66 MB 
     Shape  (576, 720)   (576, 720) 
     Count  2 Tasks  1 Chunks 
     Type  float32  numpy.ndarray

average_DT

(time)

timedelta64[ns]

dask.array<chunksize=(1,), meta=np.ndarray>

long_name :: Length of average period





  
      Array  Chunk 
  
  
     Bytes  480 B   8 B 
     Shape  (60,)   (1,) 
     Count  61 Tasks  60 Chunks 
     Type  timedelta64[ns]  numpy.ndarray

average_T1

(time)

datetime64[ns]

dask.array<chunksize=(1,), meta=np.ndarray>

long_name :: Start time for average period





  
      Array  Chunk 
  
  
     Bytes  480 B   8 B 
     Shape  (60,)   (1,) 
     Count  61 Tasks  60 Chunks 
     Type  datetime64[ns]  numpy.ndarray

average_T2

(time)

datetime64[ns]

dask.array<chunksize=(1,), meta=np.ndarray>

long_name :: End time for average period





  
      Array  Chunk 
  
  
     Bytes  480 B   8 B 
     Shape  (60,)   (1,) 
     Count  61 Tasks  60 Chunks 
     Type  datetime64[ns]  numpy.ndarray

so

(time, z_l, yh, xh)

float32

dask.array<chunksize=(1, 1, 576, 720), meta=np.ndarray>

long_name :: Sea Water Salinity
units :: psu
cell_methods :: area:mean z_l:mean yh:mean xh:mean time: mean
cell_measures :: volume: volcello area: areacello
time_avg_info :: average_T1,average_T2,average_DT
standard_name :: sea_water_salinity





  
      Array  Chunk 
  
  
     Bytes  3.48 GB   1.66 MB 
     Shape  (60, 35, 576, 720)   (1, 1, 576, 720) 
     Count  2101 Tasks  2100 Chunks 
     Type  float32  numpy.ndarray

time_bnds

(time, nv)

timedelta64[ns]

dask.array<chunksize=(1, 2), meta=np.ndarray>

long_name :: time axis boundaries
calendar :: NOLEAP





  
      Array  Chunk 
  
  
     Bytes  960 B   16 B 
     Shape  (60, 2)   (1, 2) 
     Count  61 Tasks  60 Chunks 
     Type  timedelta64[ns]  numpy.ndarray

thetao

(time, z_l, yh, xh)

float32

dask.array<chunksize=(1, 1, 576, 720), meta=np.ndarray>

long_name :: Sea Water Potential Temperature
units :: degC
cell_methods :: area:mean z_l:mean yh:mean xh:mean time: mean
cell_measures :: volume: volcello area: areacello
time_avg_info :: average_T1,average_T2,average_DT
standard_name :: sea_water_potential_temperature





  
      Array  Chunk 
  
  
     Bytes  3.48 GB   1.66 MB 
     Shape  (60, 35, 576, 720)   (1, 1, 576, 720) 
     Count  2101 Tasks  2100 Chunks 
     Type  float32  numpy.ndarray

umo

(time, z_l, yh, xq)

float32

dask.array<chunksize=(1, 1, 576, 720), meta=np.ndarray>

long_name :: Ocean Mass X Transport
units :: kg s-1
cell_methods :: z_l:sum yh:sum xq:point time: mean
time_avg_info :: average_T1,average_T2,average_DT
standard_name :: ocean_mass_x_transport
interp_method :: none





  
      Array  Chunk 
  
  
     Bytes  3.48 GB   1.66 MB 
     Shape  (60, 35, 576, 720)   (1, 1, 576, 720) 
     Count  2101 Tasks  2100 Chunks 
     Type  float32  numpy.ndarray

uo

(time, z_l, yh, xq)

float32

dask.array<chunksize=(1, 1, 576, 720), meta=np.ndarray>

long_name :: Sea Water X Velocity
units :: m s-1
cell_methods :: z_l:mean yh:mean xq:point time: mean
time_avg_info :: average_T1,average_T2,average_DT
standard_name :: sea_water_x_velocity
interp_method :: none





  
      Array  Chunk 
  
  
     Bytes  3.48 GB   1.66 MB 
     Shape  (60, 35, 576, 720)   (1, 1, 576, 720) 
     Count  2101 Tasks  2100 Chunks 
     Type  float32  numpy.ndarray

vmo

(time, z_l, yq, xh)

float32

dask.array<chunksize=(1, 1, 576, 720), meta=np.ndarray>

long_name :: Ocean Mass Y Transport
units :: kg s-1
cell_methods :: z_l:sum yq:point xh:sum time: mean
time_avg_info :: average_T1,average_T2,average_DT
standard_name :: ocean_mass_y_transport
interp_method :: none





  
      Array  Chunk 
  
  
     Bytes  3.48 GB   1.66 MB 
     Shape  (60, 35, 576, 720)   (1, 1, 576, 720) 
     Count  2101 Tasks  2100 Chunks 
     Type  float32  numpy.ndarray

vo

(time, z_l, yq, xh)

float32

dask.array<chunksize=(1, 1, 576, 720), meta=np.ndarray>

long_name :: Sea Water Y Velocity
units :: m s-1
cell_methods :: z_l:mean yq:point xh:mean time: mean
time_avg_info :: average_T1,average_T2,average_DT
standard_name :: sea_water_y_velocity
interp_method :: none





  
      Array  Chunk 
  
  
     Bytes  3.48 GB   1.66 MB 
     Shape  (60, 35, 576, 720)   (1, 1, 576, 720) 
     Count  2101 Tasks  2100 Chunks 
     Type  float32  numpy.ndarray

volcello

(time, z_l, yh, xh)

float32

dask.array<chunksize=(1, 1, 576, 720), meta=np.ndarray>

long_name :: Ocean grid-cell volume
units :: m3
cell_methods :: area:sum z_l:sum yh:sum xh:sum time: mean
cell_measures :: area: areacello
time_avg_info :: average_T1,average_T2,average_DT
standard_name :: ocean_volume





  
      Array  Chunk 
  
  
     Bytes  3.48 GB   1.66 MB 
     Shape  (60, 35, 576, 720)   (1, 1, 576, 720) 
     Count  2101 Tasks  2100 Chunks 
     Type  float32  numpy.ndarray

zos

(time, yh, xh)

float32

dask.array<chunksize=(1, 576, 720), meta=np.ndarray>

long_name :: Sea surface height above geoid
units :: m
cell_methods :: area:mean yh:mean xh:mean time: mean
cell_measures :: area: areacello
time_avg_info :: average_T1,average_T2,average_DT
standard_name :: sea_surface_height_above_geoid





  
      Array  Chunk 
  
  
     Bytes  99.53 MB   1.66 MB 
     Shape  (60, 576, 720)   (1, 576, 720) 
     Count  61 Tasks  60 Chunks 
     Type  float32  numpy.ndarray

Attributes: (6)
filename :
ocean_monthly.200301-200712.zos.nc
title :
OM4p5_IAF_BLING_CFC_abio_csf_mle200
associated_files :
areacello: 20030101.ocean_static.nc
grid_type :
regular
grid_tile :
N/A
external_variables :
areacello

2D horizontal averaging

Probably one of the most used data reduction. Since the ocean grid is not uniform, we need to weight by the cell area. Special care should also be taken with land values as we’re gonna see next. The horizontal averaging can then be computed :

\(\large \overline{tracer} = \Sigma_{i,j} (tracer ~\times~ dx ~\times~ dy ~\times~ mask) ~ / ~ \Sigma_{i,j} (dx ~\times~ dy ~\times~ mask)\)

where mask is a binary mask (0: land, 1:ocean). In MOM6 terminology, this would be written (for a tracer) as:

\(\large \overline{tracer} = \Sigma_{i,j} (tracer ~\times~ areacello ~\times~ wet) ~ / ~ \Sigma_{i,j} (areacello ~\times~ wet)\)

NB: \(\large areacello \neq dxt * dyt\), with error of a couple percent, as we can see here:

[6]:

area_diff = (ds['dxt'].fillna(0.) * ds['dyt'].fillna(0.) * ds['wet'].fillna(0.)) - \
            (ds['areacello'].fillna(0.) * ds['wet'].fillna(0.))
area_error = 100 * area_diff / ds['areacello']
area_error.plot()

[6]:

<matplotlib.collections.QuadMesh at 0x2b1d8606f630>

../_images/notebooks_spatial_operations_13_1.png

[7]:

def horizontal_mean(da, metrics):
    num = (da * metrics['areacello'] * metrics['wet']).sum(dim=['xh', 'yh'])
    denom = (metrics['areacello'] * metrics['wet']).sum(dim=['xh', 'yh'])
    return num / denom

[8]:

sst = ds['thetao'].isel(z_l=0)
mean_sst = horizontal_mean(sst, ds)

For reference, we print the first value of the obtained time-serie:

[9]:

mean_sst.isel(time=0).values

[9]:

array(18.483639, dtype=float32)

If you don’t have the “wet” array, you can infer the land/sea mask using:

[10]:

lsm = ~np.isnan(sst.isel(time=0))

and define a new function:

[11]:

def horizontal_mean_no_wet(da, metrics, lsm):
    num = (da * metrics['areacello']).sum(dim=['xh', 'yh'])
    denom = (metrics['areacello'].where(lsm)).sum(dim=['xh', 'yh'])
    return num / denom

We verify that we get the same answer:

[12]:

mean_sst = horizontal_mean_no_wet(sst, ds, lsm)
mean_sst.isel(time=0).values

[12]:

array(18.483639, dtype=float32)

[13]:

mean_sst.plot()

[13]:

[<matplotlib.lines.Line2D at 0x2b1d87abd7b8>]

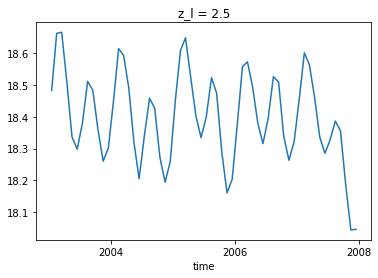
../_images/notebooks_spatial_operations_24_1.png

Zonal average

Zonal average is just a simpler case, where averaging is only done over the longitude and can be written as:

\(\large \overline{tracer} = \Sigma_{i} (tracer ~\times~ dxt ~\times~ wet) ~ / ~ \Sigma_{x} (dxt ~\times~ wet)\)

and we can define the function as:

[14]:

def zonal_mean(da, metrics):
    num = (da * metrics['dxt'] * metrics['wet']).sum(dim=['xh'])
    denom = (metrics['dxt'] * metrics['wet']).sum(dim=['xh'])
    return num/denom

[15]:

zonalmean_sst = zonal_mean(sst, ds)

If we want to plot the zonal mean, we also need to have the correct latitude array and not the so-called nominal coordinate yh. We can calculate it with the same formula:

[16]:

correct_lat = zonal_mean(ds['geolat'], ds)

Then replace the bad latitudes with the correct ones in the data array:

[17]:

zonalmean_sst = zonalmean_sst.rename({'yh': 'lat'})
zonalmean_sst['lat'] = correct_lat.values

[18]:

zonalmean_sst.isel(time=0).plot(y='lat')

[18]:

[<matplotlib.lines.Line2D at 0x2b1d87b71518>]

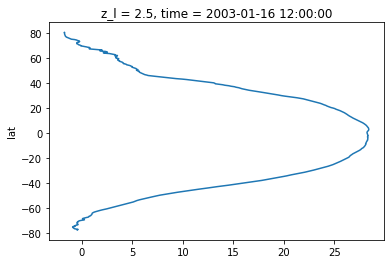
../_images/notebooks_spatial_operations_33_1.png

3D average

Same method than for the 2D horizontal average, except we use volume instead of area and sum over 3 dimensions:

\(\large \overline{tracer} = \Sigma_{i,j,k} (tracer ~\times~ dx ~\times~ dy ~\times~ dz ~\times~ mask) ~ / ~ \Sigma_{i,j,k} (dx ~\times~ dy ~\times~ dz ~\times~ mask)\)

or in MOM6 terminology, this would be written (for a tracer) as:

\(\large \overline{tracer} = \Sigma_{i,j,k} (tracer ~\times~ volcello ~\times~ wet) ~ / ~ \Sigma_{i,j,k} (volcello ~\times~ wet)\)

the function is:

[19]:

def global_mean(da, metrics):
    num = (da.fillna(0.) * metrics['volcello'].fillna(0.)).sum(dim=['xh', 'yh', 'z_l'])
    denom = (metrics['volcello'].fillna(0.)).sum(dim=['xh', 'yh', 'z_l'])
    return num / denom

[20]:

temp_global = global_mean(ds['thetao'], ds)

[21]:

temp_global.isel(time=10).values

[21]:

array(3.5970294, dtype=float32)

Let’s make the compute go a little faster with dask.

[22]:

do_full_computation = True

if do_full_computation:
    from dask.distributed import Client
    from dask.distributed import LocalCluster
    cluster = LocalCluster()
    client = Client(cluster)
    client

[23]:

if do_full_computation:
    temp_global.plot()

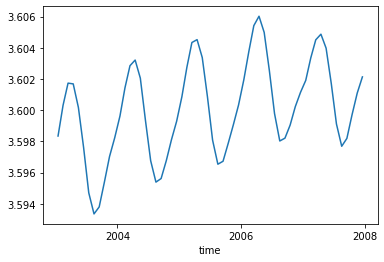
../_images/notebooks_spatial_operations_41_0.png

Using xgcm

xgcm provides some functions that perform the same computations in a elegant way. In order to get the right answers with MOM6, we need to pay particular attention to which metrics we’re using. Let’s show an example:

[24]:

from xgcm import Grid

We are pretty confident the function we wrote gives the right answer so we take it as our truth:

[25]:

sst = ds['thetao'].isel(z_l=0)
mean_sst = horizontal_mean(sst, ds)
mean_sst.isel(time=0).values

[25]:

array(18.483639, dtype=float32)

Now let’s define the xgcm grid with only \(dxt\) and \(dyt\):

[26]:

# make sure to fill in nans with zeros
ds['dxt'] = ds['dxt'].fillna(0.)
ds['dyt'] = ds['dyt'].fillna(0.)

metrics = {
    ('X',): ['dxt'], # X distances
    ('Y',): ['dyt']  # Y distances
}

coords={'X': {'center': 'xh', 'right': 'xq'},
        'Y': {'center': 'yh', 'right': 'yq'} }

grid = Grid(ds, coords=coords, metrics=metrics, periodic=['X'])

[27]:

mean_sst_xgcm = grid.average(sst, ['X', 'Y'])
mean_sst_xgcm.isel(time=0).values

[27]:

array(18.482277, dtype=float32)

Ugh not good… Third decimal is off, but remember we need to use areacello, not dxt * dyt:

[28]:

ds['areacello'] = ds['areacello'].fillna(0.)

metrics = {
    ('X',): ['dxt'], # X distances
    ('Y',): ['dyt'], # Y distances
    ('X', 'Y'): ['areacello'] # Areas
}

coords={'X': {'center': 'xh', 'right': 'xq'},
        'Y': {'center': 'yh', 'right': 'yq'} }

grid = Grid(ds, coords=coords, metrics=metrics, periodic=['X'])

[29]:

mean_sst_xgcm = grid.average(sst, ['X', 'Y'])
mean_sst_xgcm.isel(time=0).values

[29]:

array(18.483637, dtype=float32)

Now we’re consistent to the 6th decimal point.

Now with the 3d averaging, we can define a nominal layer thickness as:

[30]:

ds['dzt'] = xr.DataArray(data=ds['z_i'].diff('z_i').values,
                         coords={'z_l': ds['z_l']},
                         dims=('z_l'))

However, because of the partial steps the volume of the cell can be different from areacello * dzt so we need to add volcello to the metrics:

[31]:

ds['volcello'] = ds['volcello'].fillna(0.)

metrics = {
    ('X',): ['dxt'], # X distances
    ('Y',): ['dyt'], # Y distances
    ('Z',): ['dzt'],
    ('X', 'Y'): ['areacello'], # Areas
    ('X', 'Y', 'Z'): ['volcello'], # Volumes
}

coords={'X': {'center': 'xh', 'right': 'xq'},
        'Y': {'center': 'yh', 'right': 'yq'},
        'Z': {'center': 'z_l', 'outer': 'z_i'}}

grid = Grid(ds, coords=coords, metrics=metrics, periodic=['X'])

[32]:

%%time

mean_temp_xgcm = grid.average(ds['thetao'], ['X', 'Y', 'Z'])
# this is a bit long...

CPU times: user 18.1 s, sys: 413 ms, total: 18.5 s
Wall time: 51.6 s

[33]:

mean_temp_xgcm.isel(time=10).values

[33]:

array(3.597029, dtype=float32)

Which is in good agreement with our global_mean function!

[34]:

if do_full_computation:
    cluster.close()
    client.close()

[ ]: